Neural Networks – Activation Functions - Data Science For The Greater Good

Despite the numerous applications for neural networks and the allure of their superior performance, the main drawback of using this type of machine learning model is that not much can be done to direct how the network learns. This is another aspect of the “black box” criticism mentioned in the first post of this series. Not only do we not know what the network is doing to generate a prediction, but we also have very few avenues to direct how it learns a task.

There are, however, two main ways a data scientist can assert some influence on how a neural network learns: activation functions and optimizers. The selection of these two aspects should garner considerable thought as they can significantly affect model performance. The focus of this post will be the pros and cons of several activation functions. Various optimizers will be covered in a subsequent post as they pertain more to back propagation.

Activation Functions

Activation functions are transfer functions within neural networks that map the output of one node to the input of the next node. When compared to the biological neuron, activation functions can be thought of as action potentials as they propagate the data through the network. There are many to choose from and often iterating through several candidates is the best method for determining which one will work best. But, because neural networks require large amounts of data, training is both resource and time consuming. Thus, it is essential to understand how each function transforms the data and how its derivative could affect the network’s ability to learn in order to narrow down selection of “best candidates” for any particular task.

Sigmoid

The sigmoid function is one of the most common activation functions used in the output layer of binary classification tasks. This is because it transforms the data to a number between 0 and 1, which translates nicely to class probability (think logistic regression). However, as the values of z (product of the linear transformation within a node) get larger in the positive direction or smaller in the negative direction, the derivative of the sigmoid function at those points approaches zero. This scenario is known as a vanishing gradient. Because the derivative of the activation function is used during back propagation to update the weights and bias values, a derivative approaching zero significantly slows down the learning rate of the network at these nodes.

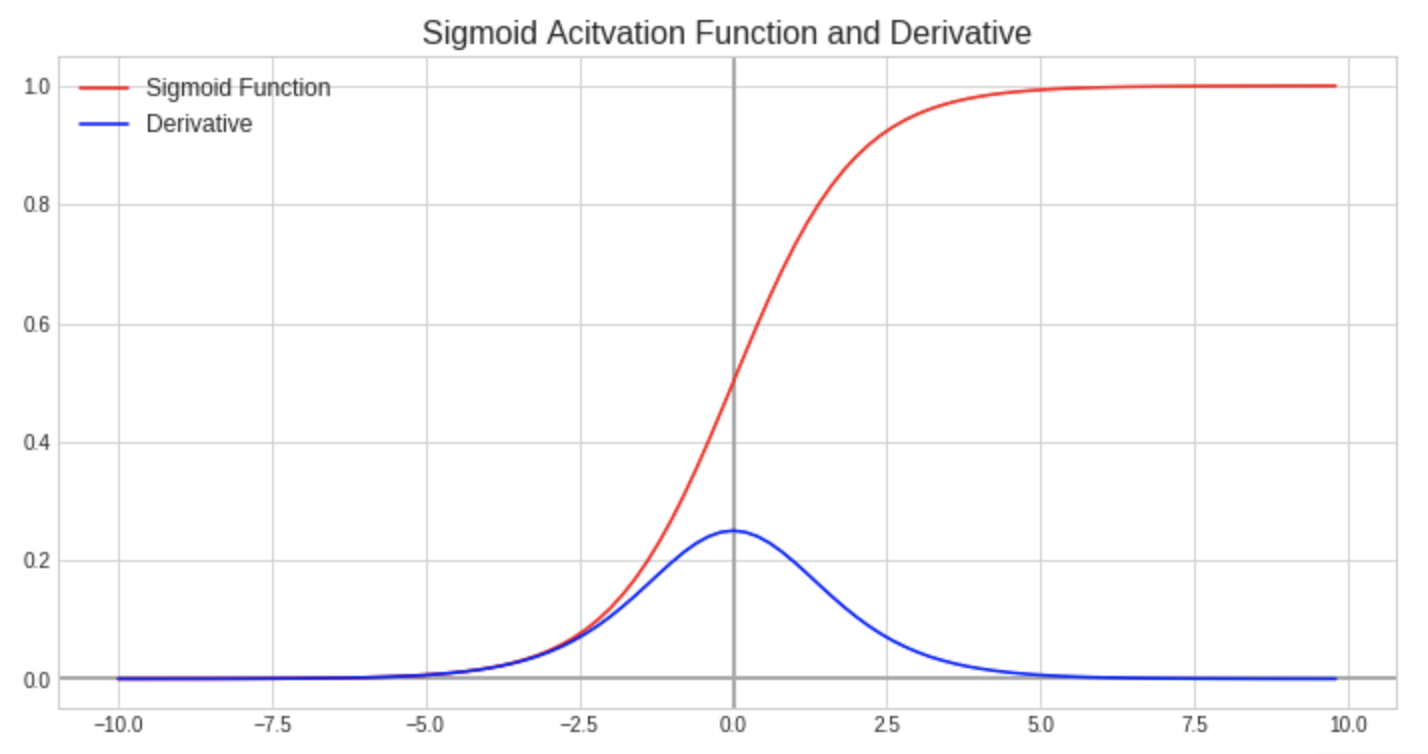
Hyperbolic Tangent (tanh)

The hyperbolic tangent function is very similar to the sigmoid function except that it outputs values between -1 and 1, which makes optimization a little easier because it centers the data around zero. For this reason, the tanh function is typically used in the hidden layers for binary classification tasks. The vanishing gradient issue described for the sigmoid function is actually more pronounced in the tanh function as its tails approach their asymptotes along a much steeper curve, resulting in a derivate that approaches zero over a much shorter range than the derivative for the sigmoid function.

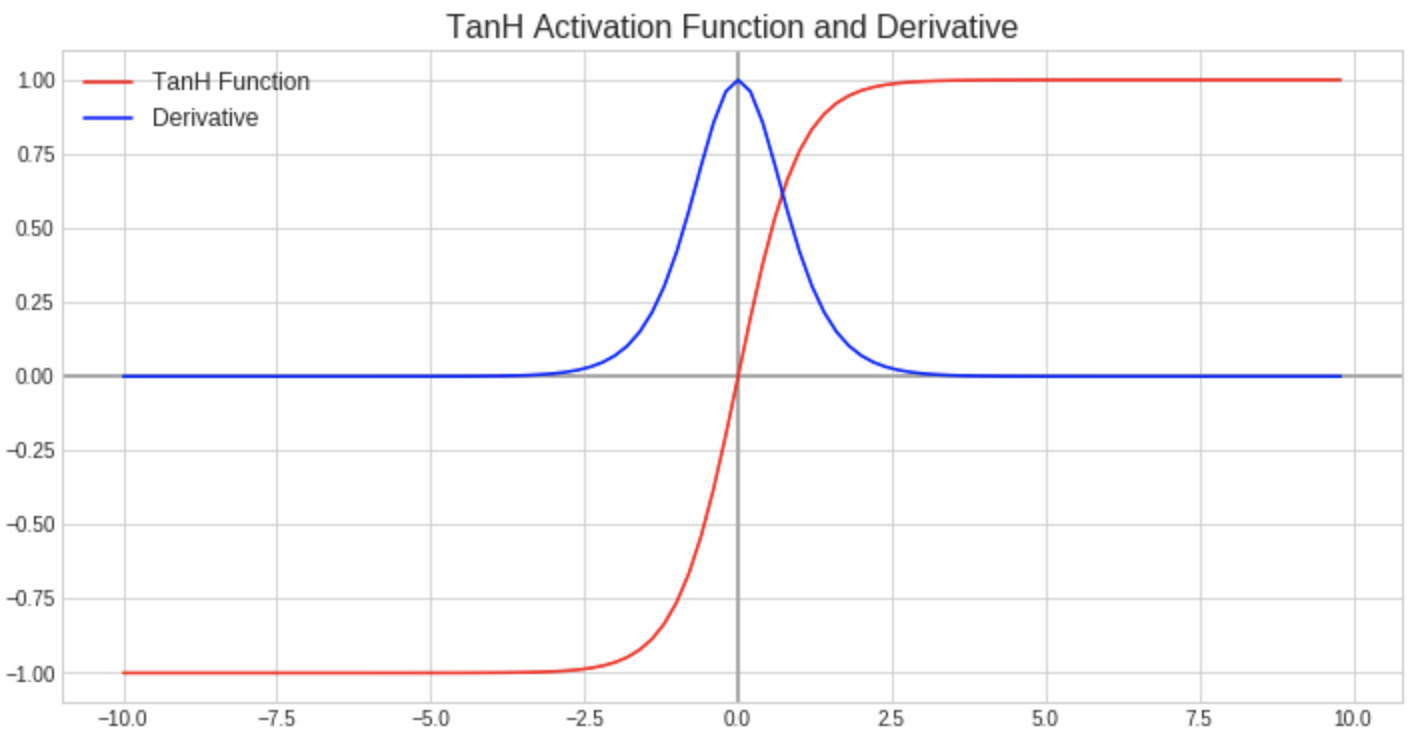
Inverse Tangent (arctan)

The inverse tangent function attempts to maintain the positives from the tanh function while also addressing the vanishing gradient issue. It outputs values between -pi/2 (-1.6) and pi/2 (1.6), keeping the optimization benefits of zero-centered data. Also, the function’s curves approach their asymptotes more gradually, which persists a gradient in the derivative over a larger range. Though, the derivative of the arctan function is more computationally expensive to compute, which will add to the resources and time needed to train a model employing this activation function.

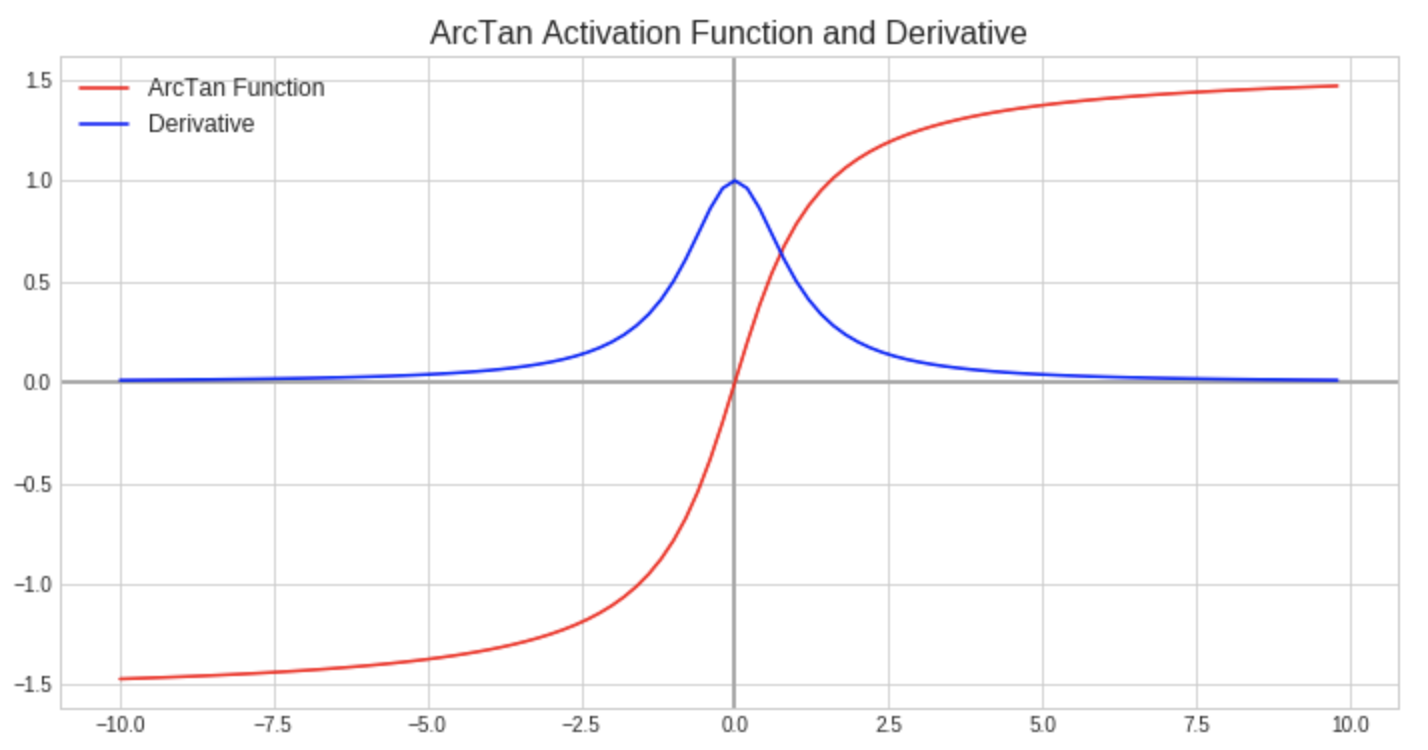
Rectified Linear Unit (ReLU)

The rectified linear unit is currently the most popular activation function as it retains the biological motivation of an action potential (node will only “fire” if the input exceeds a threshold) and it typically yields superior results to the three activation functions previously mentioned. It outputs values in the range of zero to infinity as all negative inputs will result in an output of zero and all positive inputs are without bounds along a linear function. The simplicity of this function makes it easy to calculate its derivative, reducing necessary resources and training time, but it can result in neurons that are unable to update their weights and bias values (dead neurons) if their z values are negative.

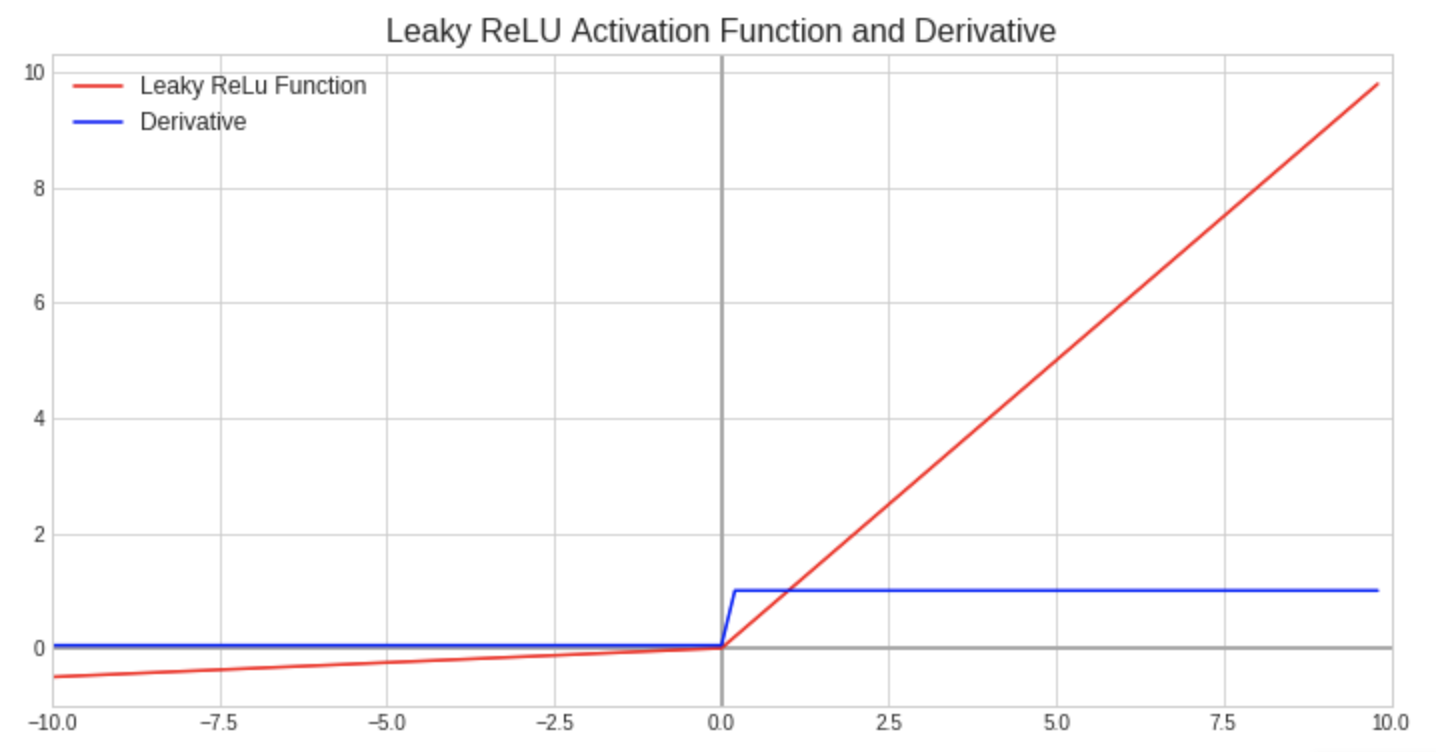
Leaky Rectified Linear Unit (Leaky ReLU)

The leaky rectified linear unit is a variant of the ReLU function that allows for a small positive slope (normally 0.01) for z values less than zero. While the slope is small, thus making learning slow, this variation eliminates the dead neuron issue present with the ReLU function.

Softmax

The softmax function is very popular for multiclassification tasks. It outputs a vector of values between 0 and 1, where each element in the vector represents its probability of belonging to a particular class. Thus, the total sum of the output vector will equal 1 and the class represented by the largest element in the vector will be the model’s predicted class. For this reason, the softmax function is typically used in the output layer of neural networks learning multiclassification problems.

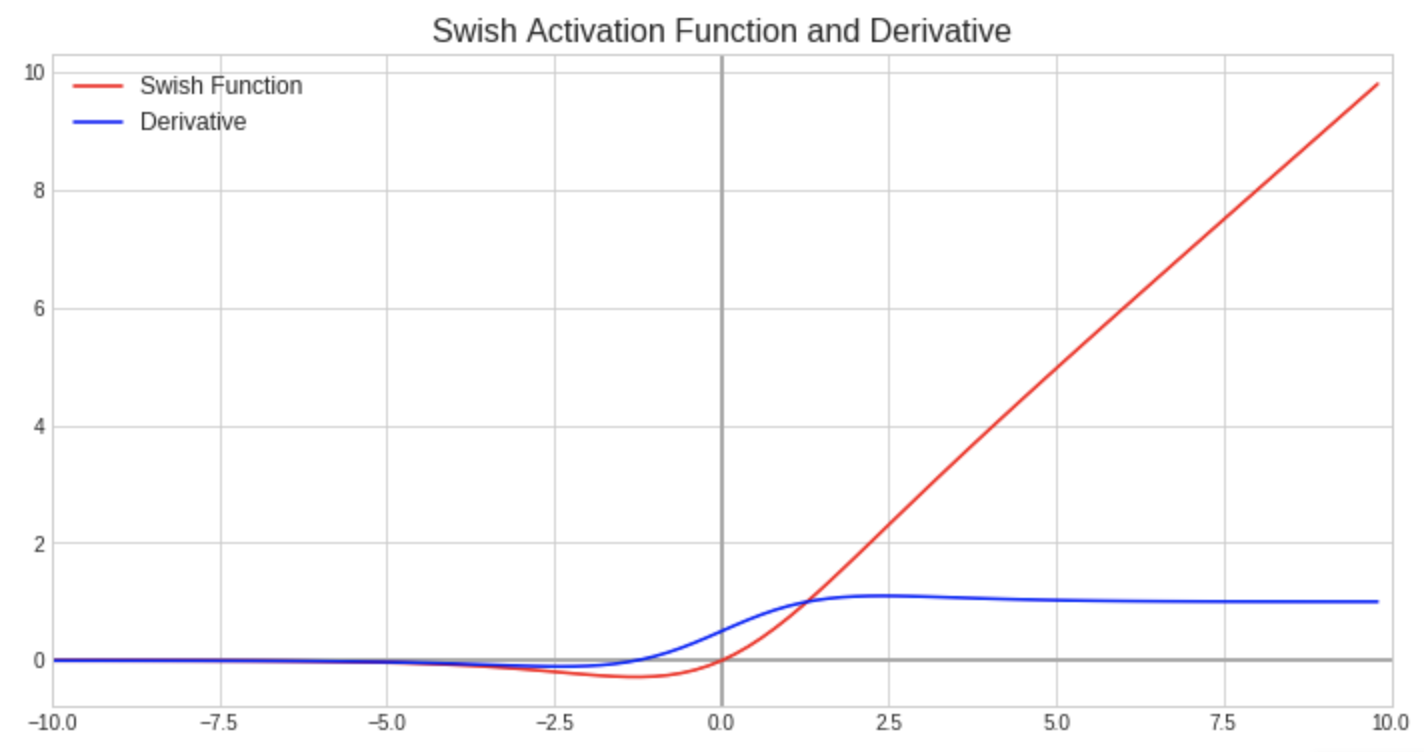
Swish

The swish activation function was developed by Google in 2017. It has been described as a self-gated function and has shown marginal performance increases over ReLU for computer vision tasks. While the overall performance of this “new kid on the block” is still up for debate, it does address the dead neuron problem present with the ReLU function. Also, it is unique from all other activation functions in that it is non-monotonic (specifically for the region of the function pertaining to z < 0). This means its output could decrease in value even though the input is increasing. However, it is more computationally expensive than ReLU and may increase training time.

Summary

There are numerous activation functions to choose from when constructing a neural network, with more in development. Having an understanding of how these functions operate within neural networks is crucial to building high-performing models efficiently. While the activation functions mentioned in this post by no means form a comprehensive list, they are the most popular ones in use today. The next post will cover the other major means of influencing learning within a neural network, optimizers.